調号とは、よく楽譜のト音記号の横にいくつか♯や♭がついていますが、あれです。この♯や♭のつき方(調号)で、曲のキーがわかります。
#のつく順番や♭のつく順番は決まっていて、#の場合、ファ、ド、ソ、レ、ラ、ミ、シの順番についていきます。♭の場合は、これと反対で、シ、ミ、ラ、レ、ソ、ド、ファの順番についていきます。そして、♯や♭が何個ついているかでキーがわかります。なぜ順番が決まっているのか、他のバリエーションはないのか等、紹介していきます。
Contents
#系の調号
まず#系を説明しましょう。#系とはト音記号の横に#がいくつかついている調号です。

なにもついてないときのキーはC(ハ長調)ですね。これに#が1個つくとキーがG(ト長調)になります。#の場所はファ#です。2個つくとD(ニ長調)です。#の場所はファ#とド#です。3個つくとA(イ長調)、4個つくとE(ホ長調)、5個つくとB(ロ長調)、6個つくとF#(嬰ヘ長調)です。(このF#は♭が6個ついたG♭の変ト長調と同じになります。)「嬰」というのは調を示すイロハニホヘトにシャープが付いているという意味になり、「えい」と読みます。嬰ヘ長調は「えいへちょうちょう」と読みます。
調号のシャープがひとつ増えるたびに、キーが5度ずつ上がっていきます。Cの調号に♯が1個つくと、Cから5度あがってGになります。Gの調号にもうひとつ♯がつくと、Gから5度あがってD、という感じです。
♭系の調号
次に♭系を説明します。♭系とはト音記号の横に♭がいくつかついている調号です。

なにもついてないときのキーはCですね。これに♭が1個つくとキーがF(ヘ長調)になります。♭はシに付きます。2個つくとB♭(変ロ長調)です。♭の場所はシ♭とミ♭です。3個つくとE♭(変ホ長調)、4個つくとA♭(変イ長調)、5個つくとD♭(変ニ長調)、6個つくとG♭(変ト長調)でF#(嬰ヘ長調)と同じになります。「変」というのは調を示すイロハニホヘトにフラットが付いているという意味になり、「へん」と読みます。
こちらは、♭が突くたびに4度あがりますが、5度下がると考えた方が良いです。Cに♭がつくと5度下がってFになります。Fにもうひとつ♭がつくと5度下がってB♭、という感じです。
♯がついたり、♭がつくと5度変わるということは、後で述べるドミナントモーションと深い関係にあります。調号と一緒にドミナントモーションも覚えてしまうことをお勧めします。
短調の場合は?
調(キー)には、短調(マイナーキー)というのもあり、同じく調号が存在します。ですが、短調の場合はそれと平行調となる長調の調号と全く同じになります。C調の調号とAm調の調号は同じですし、G調とEm調の調号は同じです。それぞれの対応表を書きます。まず#系の調号です。
| #の数 | 長調 | 短調 |
| 0 | C(ハ長調) | Am(イ短調) |
| 1 | G(ト長調) | Em(ホ短調) |
| 2 | D(ニ長調) | Bm(ロ短調) |
| 3 | A(イ長調) | F#m(嬰ヘ短調) |
| 4 | E(ホ長調) | C#m(嬰ハ短調) |
| 5 | B(ロ長調) | G#m(嬰ト短調) |
| 6 | F#(嬰ヘ長調) | D#m(嬰ニ短調) |
次にフラット系の調号です。
| ♭の数 | 長調 | 短調 |
| 0 | C(ハ長調) | Am(イ短調) |
| 1 | F(ヘ長調) | Dm(ニ短調) |
| 2 | B♭(変ロ長調) | Gm(ト短調) |
| 3 | E♭(変ホ長調) | Cm(ハ短調) |
| 4 | A♭(変イ長調) | Fm(ヘ短調) |
| 5 | D♭(変イ長調) | B♭m(変ロ短調) |
| 6 | G♭(変ト長調) | E♭m(変ホ短調) |
なぜ同じ調号なのに長調と短調が存在するのか?全部長調でいいんじゃないか?と思うこともあるかもしれません。ここはモード(教会旋法)で詳しく解説していますが、簡単に言うと長調は明るい感じを作り出し、短調は暗い感じを作り出す違いがあります。何の音を起点にするかで曲のイメージが変わります。
なぜ順番が決まっているのか?
ここまで説明したように、調号の#や♭は増える順番が決まっています。なぜこんなに規則的に決まっているのか、#や♭の付き方はもっとバリエーションがあるような気もします。また、なんで5度ずつ規則的に変わっていくのかという点も面白いです。ここでは、そんな疑問を解消していきます。
まず長調の音階は、下の図にあるように音程のインターバルが、全全半全全全半、となっています。ミファの部分とシドの部分が半音階となっています。
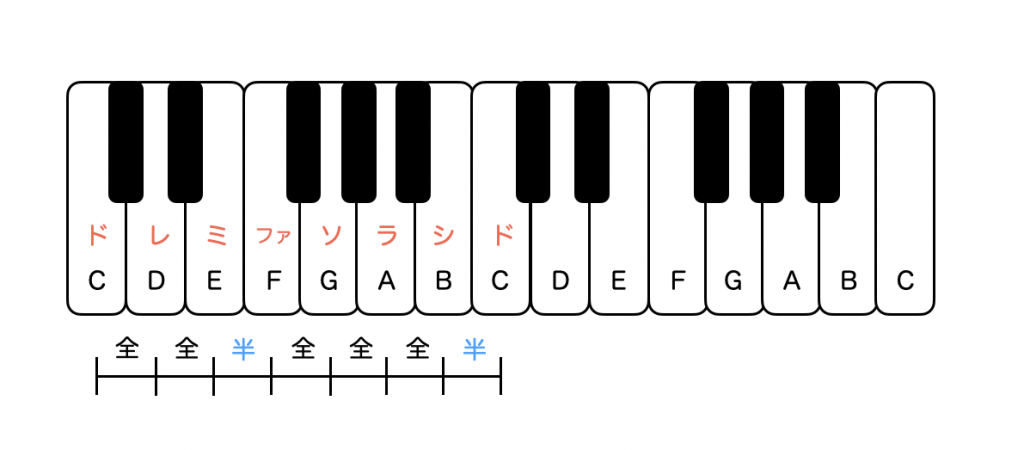
この「半」の位置をランダムに変えれば、いろんなバリエーションの#や♭の調号が作れそうですが、それだと長調にならないので、「半」と「半」の間には「全」が2つおよび3つ入るという条件を満たさなければいけません。そうなると必然的に12通りの調号しかなくなります。
次に、どうして調号の#や♭は増える順番が決まっているのかですが、これはいくつかやってみるとわかります。上の図でミファとシドが半音階なので、シドのところがミファになるようにしてみましょう。
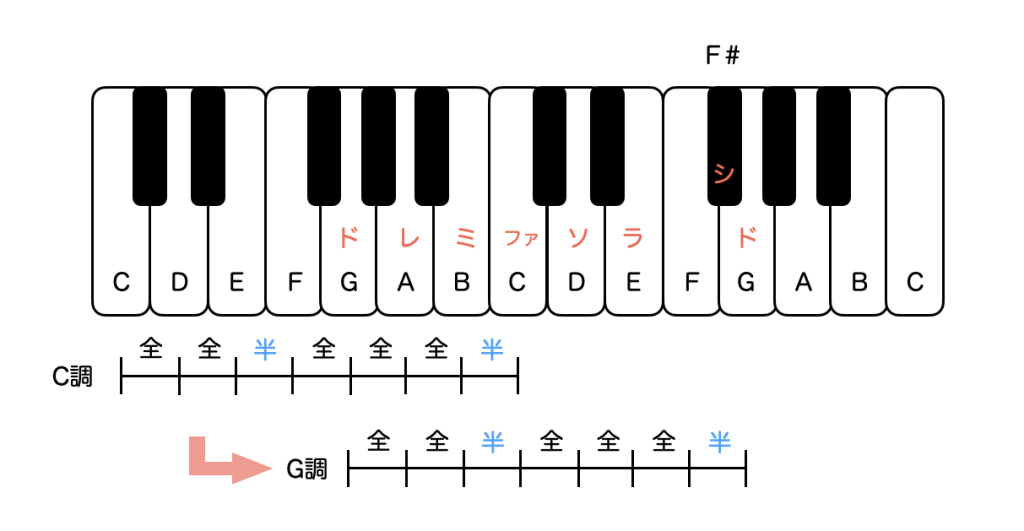
シドのところにミファを持ってくると、Gがドになり、Gを起点としたドレミファソラシドになり、G調(ト長調)になります。ただ、シドの部分は半音階なので、FをF#にしなくてはいけなくなります。なので、G調(ト長調)はファに#がついた調号になります。
次にもう一段階進んで、G調で考えたドレミファソラシドのシドのところにG調のミファを持っていくことをしてみます。
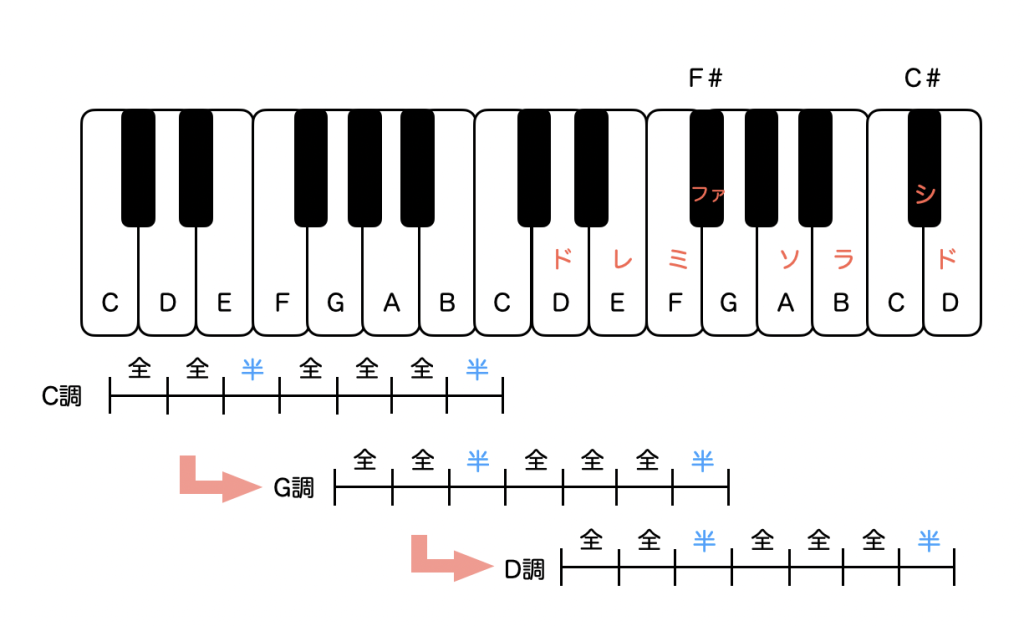
すると、Dがドとなり、Dを起点としたドレミファソラシドになります。ここでもやはりシドの部分を調整する必要がでてきて、シドは半音階なのでCをC#にする必要があります。F#は半音階で合わせてるのでここは変わらずです。つまり、D調(ニ長調)の場合は、ファとドに#がついた調号になります。
このように、「ミファ」が「シド」になるようにずらすと、調の起点がC→G→Dと5度ずつあがり、#がひとつずつ増えます。数学的帰納法(?)により、これを12回やれば全ての調号を経験しながら元のC調に戻ります。ですが、#で表記するのは6回までです。(たまに7回目のシャープ調号もありますが)それ以上はフラットの調号で表記します。
上記は「ミファ」が「シド」になるようにずらしました。これは変化をひとつだけにするため片方の半音階を半音階のままにするためです。同様にこのルールでもうひとつずらせる方法があります。「シド」が「ミファ」になるようにしてもひとつしか変化しないようにできます。この場合は、5度下がり、フラットがひとつ付く(#がひとつ消える)変化になります。C調からはじめると、C→F→B♭となり、F調の場合はシがフラット、B♭調の場合はさらにミもフラットと、フラットがひとつずつ増えていきます。
では、なぜ一度#(♭)になったものはずっと#(♭)なのかというと、そもそもこのずらし方で考えると、#(♭)の変化がひとつしか起きないようにしています。つまり#(♭)が増えるか消えるかです。もし5度上げて、今までの#のどれかが消えるようなことがあったら、そこだけでひとつの変化となり、他は変えられないことになります。そうなると5度下の調と同じになってしまい矛盾するため、5度上げる変化において一度#になった音はずっと#が付きます。