なぜ12音階なのか？

音楽をやっていて、何故、音階は12種類なんだろう？って思ったことはありませんか？ピタゴラスが発見したらしいのですが、算数とちょっとした物理がわかれば自分で発見できる方もいらっしゃると思います。

ここでは、少しずつヒントを書きながら説明していきますので、是非、考えてみてください。「なるほど12が一番いい！」となったら完全理解です。

スタート問題

まず、前提知識として、音程は、音波の周波数で決まります。この周波数の比が簡単な整数比になっている音同士は調和します。そして、以下の2つの定理から始まります。

• 周波数の比が１：２になると、ものすごく調和する。
• 周波数の比が１：３になると、けっこう調和する。

人間の鼓膜が弦振動のような構造だからでしょうか。ここは、こういうものだと疑わずに進んでください。

この2つの条件だけで、12音階が導かれます。これだけでわかったら、ピタゴラス並のIQを持っていると思います。

ヒント1

では、最初のヒントですが、上の定理を、現在の12音階の音楽にあてはめて考えますと、

• 周波数が2倍になると、音程がオクターブ上がる。
• 周波数が3倍になると、オクターブと5度上がる。

図に書いてみます。

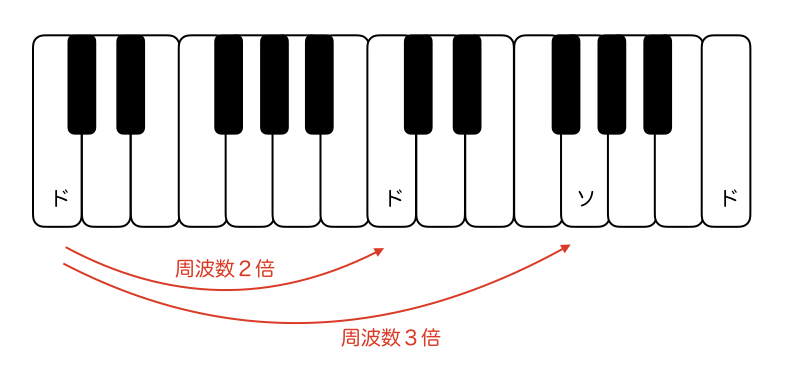
ドの音の周波数を2倍にした音は、オクターブ上のドになっています。そして、ドの音の周波数を3倍にした音は、オクターブと5度上のソになっています。ドとドが調和するのはわかると思います。ソは、ドに対してドミナント音なので、ドの次に調和するものなのです。このヒントだけで12音階が導けるか是非考えてみてください。

ヒント2

次のヒントですが、周波数3倍のソ（5度）の音に着目します。周波数2倍でオクターブ上がるということは、周波数0.5倍でオクターブ下がるということです。ですので、周波数3倍のソの音の周波数を半分にすると、オクターブ下のソの音になります。この音は、基準としたドの音に対して、3倍×0.5倍なので、1.5倍になっています。つまり、1.5倍するごとに5度あがるわけです。図に書いてみます。

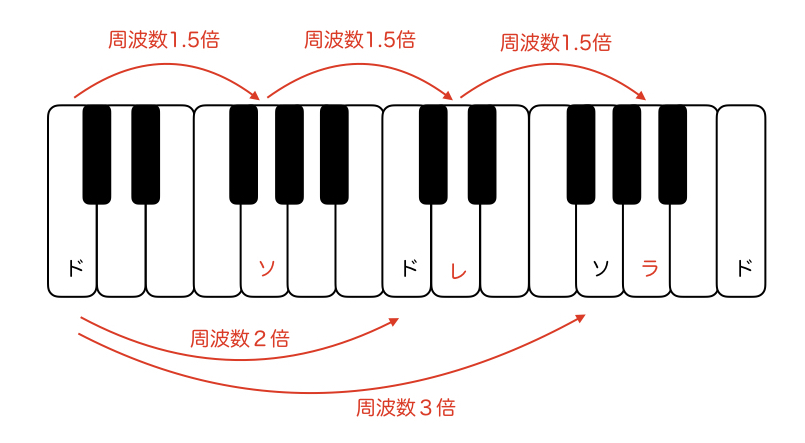
ソの音に対してさらに1.5倍すると、ソから5度上がったレになります。レをさらに1.5倍すると、レから5度上がったラになります。（5度というのがわかりにくい場合は、半音階7個分と考えてみてください。）このヒントで12音階が導けるか考えてみましょう。ドミナントモーションに似てるなと思った方、ほぼゴールまで来てます。

ヒント3

上のヒントから、ずっと1.5倍していくとどうなるか考えてみましょう。まず、1.5倍を2回すると、2.25倍になりますね。では、1.5倍のべき乗の値を下の表に書いてみます。小数点3桁目を四捨五入して、少数2桁で書きます。

1.5のべき乗数	値（倍数）
1	1.5
2	2.25
3	3.38
4	5.06
5	7.59
6	11.39
7	17.09
8	25.63
9	38.44
10	57.67
11	86.50
12	129.75
13	194.62
14	291.93

1.5倍を12回した1.5の12乗の値を太字で書いてみました。何かピント来ませんか？ヒントは、「人間、ちょっとぐらい周波数がずれても気づかない」です。近い整数を考えてみましょう。

ヒント4

上のヒントで、1.5の12乗が129.75ということがわかりました。2のべき乗が頭に入っている方は、「128だったらなー、おしい！」思いませんか？もし128だったとしたら、128は2の7乗なので、1.5倍を12回して音を上げていくと、7オクターブ高い同じ音に戻るわけです。129.75は128の約1.01倍です。1%違うだけです。人間の鈍感力を使い、もう同じことにしちゃいましょう。図に書いてみます。

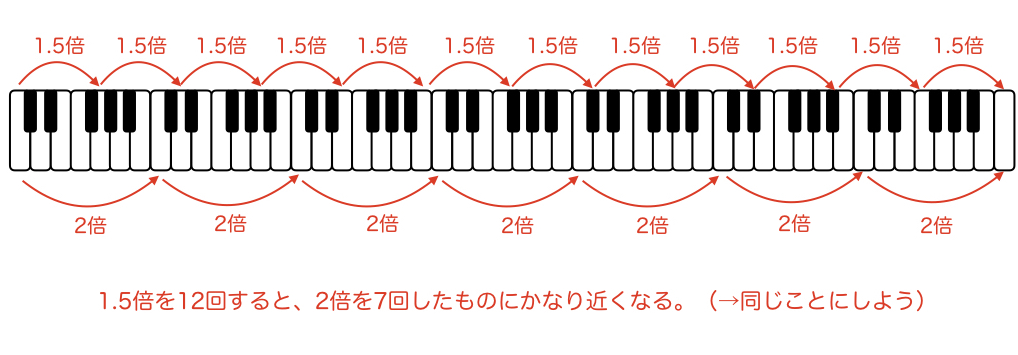
この図から、音階が12種類であることがなんとなくわかったでしょうか？もうほとんどゴールまで来てます。

解説

1.5倍ずつ音を上げていくと、初めて同じ音に戻るのは12回上げた時です。つまり最初の基準音を含めて12種類の音を経由して元の音に戻るわけです。これらの経由した音は周波数を半分、1/4等にしていくと、最初のオクターブ内の音に戻すことができ、全て違う音になります。なので、ピタゴラスはオクターブ内の音を12種類に分けようと考えたわけです。ただ、1%の誤差がありますよね。この誤差を12種類の音に均等に分配するのが平均律という現在の音楽で使われているものです。よく使う音（ド、ミ、ソ等）だけはぴったり合わせて、他の音で誤差を調節しようというのが、純正律です。ですが、この純正律だと、転調したらよく使う音も変わってしまうため、やはり平均律が使いやすくて使われているというのが現状です。

この平均律を用いると、オクターブの音を同じ比で12等分するため、隣の音との周波数の比は、2の12乗根になります。図に書いてみます。

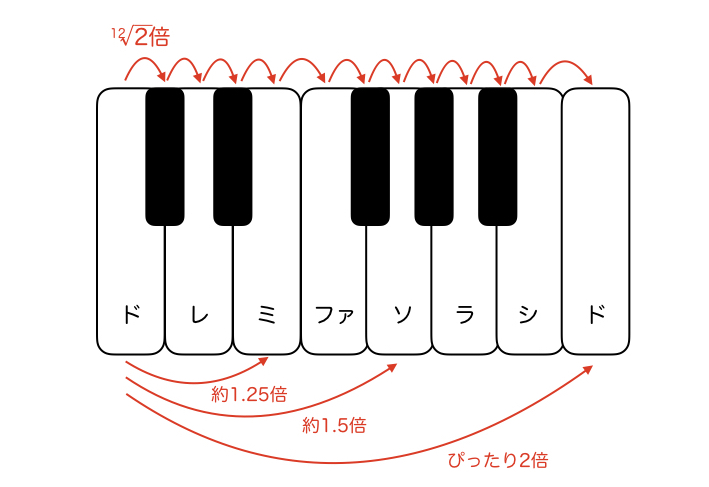
このような感じになり、完全5度のソは約1.5倍、長3度のミは約1.25倍になっています。Cメジャーコードの構成音は、ド、ミ、ソですね。この構成音の周波数の比は4:5:6ときれいな整数比になっております。これがメジャーコードの周波数比であり、心地よく調和する理由です。

2の12乗根を倍々にしていった数値を表にも書いてみます。

2の12乗根のべき乗数	値（倍数）	音程（ドを基準にした場合）
1	1.0594	短2度
2	1.1224	長2度
3	1.1892	短3度
4	1.2599	長3度（ミ）約1.25倍
5	1.3348	完全4度（ファ）約4/3倍
6	1.4142	減5度
7	1.4983	完全5度（ソ）約1.5倍
8	1.5874	短6度
9	1.6817	長6度
10	1.7817	短7度
11	1.8877	長7度
12	2.0000	完全8度（ド）2倍

赤字で書いたところが、基準音に対して特に調和する音で、基準音がドとすると、ミが約1.25倍、ソが約1.5倍で、ド・ミ・ソの和音が、4:5:6の周波数比になっていることがわかります。この和音の構成音のソをオクターブ下げて、ソ・ド・ミという構成音で考えてみると、ソが6⇨3になるため、3:4:5 という美しい周波数比にもなります。

3、4、5って、直角三角形の条件であるピタゴラスの定理でよくでてくる数ですね。この12音階もピタゴラスが作ったものです。偶然でしょうか、なにか関係があるのでしょうか。

以上、なぜ12音階なのか？の説明でした。物理と数学と音楽の話が混ざったお話でした。改めて音楽って美しいなって思います。