The flute’s clear, airy tones contrast beautifully with the warm, resonant sounds of the guitar, creating a dynamic interplay that captivates listeners.
When a flute and guitar play together, their distinct timbres merge harmoniously, blending high-pitched melodies with deep chord progressions to produce a balanced, multifaceted musical experience.
The unique pairing of flute and guitar allows for a diverse range of musical expressions, from gentle and introspective passages to lively and rhythmic motifs that showcase the versatility of both instruments.
Composers and musicians often leverage the complementary nature of flute and guitar to craft compositions that explore contrasting moods and emotions, resulting in compositions that resonate deeply with audiences.
Beyond their sonic differences, the flute’s melodic agility complements the guitar’s harmonic foundation, creating a synergy that enriches both instruments’ capabilities and expands the possibilities for musical collaboration.
Let’s explore why this is.
Waveform of Flute and Guitar
First, let’s compare the waveform of a flute sound with that of a guitar sound.
For reference, let’s compare these waveforms with that of a sine wave. A sine wave, being the simplest waveform with only one frequency component, appears as a smooth, regular oscillation without any additional harmonics or overtones. This comparison highlights the fundamental differences in the complexity and richness of sound between the flute and guitar.
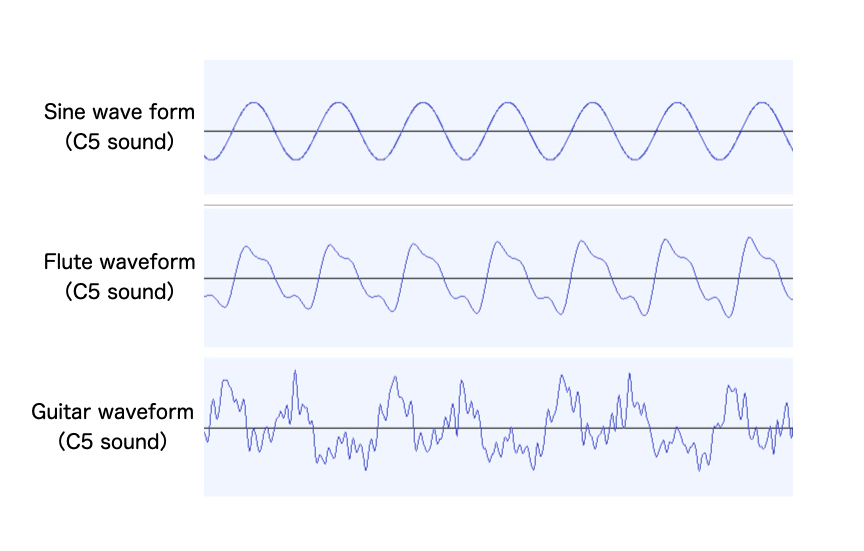
All of the waveforms are for C5, which is a C note in the middle register.
The top one is a sine wave form. It has an exact simple wave shape.
In the middle is the waveform of the flute sound. This waveform exhibits a slight variation in shape due to the overlapping of its harmonic waves, but it closely resembles a sine wave. Among musical instruments, the flute is considered one of the closest to producing a sine wave in its fundamental tone. Instruments like the ocarina and recorder also share this characteristic, where their waveforms maintain a relatively smooth and simple pattern, emphasizing their pure and clear tonal quality. This similarity to a sine wave contributes to the flute’s distinctive clarity and its ability to blend seamlessly with other instruments, creating a balanced and harmonious sound in musical compositions.
At the bottom is the waveform of the guitar sound, characterized by its complex nature. This waveform results from the blending of numerous harmonic waves. Unlike the flute, the guitar’s waveform deviates significantly from a sine wave due to the intricate interplay of its overtones and harmonics. Despite this complexity, when heard, both the flute and guitar produce sounds at the same pitch, showcasing the remarkable ability of the human ear to discern pitch even amidst varying waveforms. This phenomenon highlights the ear’s capacity to perceive and appreciate the tonal richness and complexity of musical instruments, contributing to our enjoyment and understanding of music as a whole.
Harmonics
I mentioned at the beginning that tone is determined by the balance of harmonics. Let me explain this in terms of frequency spectrum.
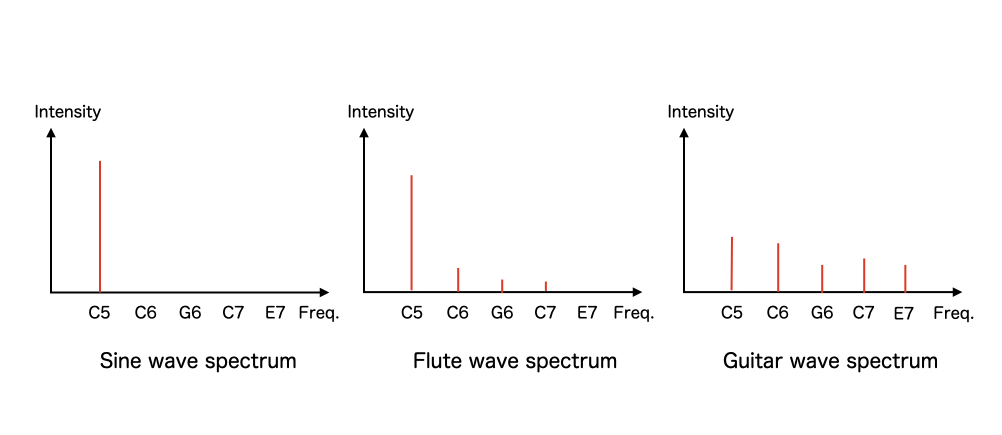
First, the spectrum of a sine wave, which is a wave of a single frequency, so in the above example, only C5 (523 Hz) has the intensity of the spectrum.
The frequency spectrum of a flute is similar to the spectrum of a sine wave, but it contains some harmonics. But basically, the spectrum of C5, the reference frequency, can be made stronger.
In contrast, the frequency spectrum of the guitar has an overall spread in the intensity of the various harmonics, and the spectrum seems to be rolling and spreading out horizontally.
I believe that the combination of this vertically sharp flute and the horizontally gentle guitar creates an ensemble that is both expansive and sharp.
The horizontal axis is the frequency. Only the pitch of the harmonic overtone is written. In this example, for the reference note of C5, we have the following harmonics.
- 2nd Harmonics(C6) C
- 3rd Harmonics(G6) G
- 4th Harmonics(C7)C
- 5th Harmonics(E7)E
There are of course more than 6th harmonics, but I’ve simplified it. Basically, harmonics of frequencies are integer multiples of the reference frequency.
I was actually going to post a Fourier transform diagram, but since there are components other than orthogonal frequencies, it was difficult to understand (especially for guitars), so I made an image diagram.
The lowest note of the flute is C4 (about 261 Hz), which is the note of C on the third fret of the fifth string on the guitar. Therefore, when the flute is playing a low note, the frequency will be overlapped by the chord playing in the low position. Therefore, when the flute is playing low notes, I try to play the guitar gently and conservatively with arpeggios.
Flute and Guitar Ensemble
The lowest note of the flute is C4, approximately 261 Hz, equivalent to the note C on the third fret of the fifth string on the guitar. This means that when the flute plays low notes, its frequency range overlaps with the chords played in lower positions on the guitar. To accommodate this, I approach playing the guitar gently and modestly, using techniques like arpeggios. This ensures that the guitar supports the flute without overpowering it, allowing both instruments to blend harmoniously. By emphasizing arpeggios and softer playing in lower registers, the guitar complements the flute’s melodic lines, creating a balanced and cohesive musical texture that enhances the overall performance.
I hope you can feel the possibilities of the flute and guitar.